Constantly improving the communication capacity and quality of communication systems is an eternal theme of wireless communication. With the rapid development of wireless communication technology, people have put more and more demands on the design of the antenna. Ultra-wideband (UWB) technology and Multiple Input Multiple Output (MIMO) technology have great potential for improving data transmission rate. MIMO technology can improve the signal-to-noise ratio of communication systems, improve channel capacity and suppress channel fading for mobile devices. In this case, the need to integrate multiple units together to reduce the size of the entire antenna requires a low mutual coupling between the MIMO multi-antenna units to achieve low correlation between the signals. The feature mode technique based on the moment method is the best choice. The eigenmode analysis method is an analytical method that has emerged in recent years. It is a new method that uses a wide range of moment methods combined with analytical eigenmode theory to solve electromagnetic problems. It provides an optimal antenna design for antenna designers to help antenna designers understand how antennas work. Using the different mode information obtained by the analysis, grasping the resonance characteristics and the radiation characteristics of different modes, and selecting the optimal feeding position by using the distribution of the characteristic currents of different modes to stimulate the required mode, it also helps to guide the designer. The antenna is slotted to fine tune its resonant position [1]. In this paper, the characteristic mode parameters of several common antenna forms are simulated by FEMO V14 version [2]. The mode method defines a series of eigenmodes similar to the analytical method for electromagnetic problems of arbitrary complex shapes. These modes can describe the intrinsic properties of electromagnetic problems, and the orthogonal characteristics between the modes, the size of the eigenvalue directly determines The contribution of this mode to electromagnetic parameter parameters. It makes the moment method have a clearer physical vision, and the antenna designer can use the information provided by the pattern analysis to understand the working principle of the antenna more deeply, design the antenna with the best performance, and even design a new antenna form [3] ]. The eigenmode theory was originally proposed by Garbacz in his PhD thesis [4] in 1968. In 1971, Harrington and Mautz obtained the same pattern defined by Garbacz by the generalized impedance matrix of diagonalized conductors [5]-[6] The formula called the characteristic mode theory described in [5] is easier to derive than that proposed by Garbacz [4], and it is very effective to verify the structure of an arbitrary shape. Harrington et al. later extended the eigenmode theory to handle electrolytes, magnetic media, and electrical/magnetic hybrids [7]. Since the introduction of the characteristic mode theory, it has received extensive attention in the fields of computational electromagnetics and antenna design. The eigenmode theory defines a series of mutually orthogonal feature patterns for conductors of arbitrary shape, and these mutually orthogonal feature modes are inherent properties of the conductor, which have convergence and completeness, and can accurately represent the solution of the electromagnetic problem. The physical model of the eigenmode theory is clear, and the working mechanism of the electromagnetic structure can be clearly given. At the same time, the characteristic mode is only related to the shape, size and working frequency of the electromagnetic structure, and has nothing to do with the source point, so it is convenient to guide the engineering design. The eigenmode theory is based on the MoM method, and its eigenequation is: The current on the conductor is developed using the characteristic current as a basis function: In addition, after derivation: The expansion factor αn in Equation 2.3 represents the characteristic current Since R and X are both HermiTIan operators and also real symmetric operators, the operator R is a positive definite operator. Therefore, the eigenvalue λn and the characteristic current Jn obtained from the generalized eigenvalues ​​and the properties of R and X are real numbers. (ie in phase). It can be shown that the characteristic current satisfies the following orthogonality [30]: <Jm , RJn>=δmn (2.5-1) <Jm , XJn>=λnδmn (2.5-2) <Jm , ZJn>=(1+jλn)δmn (2.5-3) Here, the characteristic current is normalized, that is, <Jn , RJn>=1. Indicates that the radiated power is 1. Since Pmn=<Jm , ZJn>, in the case of radiant power of 1, the energy storage is only related to λn, and the sign of λn determines the type of energy storage: when λn is closer to 0, it means that the mode is at this frequency. Near resonance; λn>0 means that the mode stores magnetic energy at this frequency; λn<0 means that the mode stores electrical energy at this frequency. Since the value of λn varies greatly, it is not convenient to observe. The Modal Significance (MS) and the characteristic angle Characteris TIc Angle (CA) are also used to represent the resonance of each mode of the antenna: CA=180° -tan-1 λn (2.6-2) It can be known from equation (2.6-1) that the value range of MS is (0,1). When the MS is closer to 1, it indicates that the mode is closer to the resonance state; on the contrary, it indicates that the mode is far from resonance and is difficult to be excited and effectively radiated. From (2.6-2), when CA = 180 degrees, it means that the mode is a resonance state. The MS parameter can be used to define the radiation bandwidth BWn of the mode, that is, the frequency range in which the radiant energy is greater than or equal to half the radiant energy of the resonance point in the frequency band. The above equations fU and fL are the two frequency points when the MS value is 0.707, and the fres is the resonance frequency of the current mode. The bandwidth can be calculated by (2.7-2). Similarly, the working bandwidth of each mode can also be The characteristic angle (CA) is read out from the curve of the frequency change, and it is not difficult to obtain that when the MS value of each mode is 0.707, the corresponding λn=1 and λn=-1, CA=135 degrees and CA=225 degrees. Through the characteristic mode analysis, the eigenvalue (λn), characteristic current (Jn), characteristic angle (CA), and mode current coefficient MS of each mode of the antenna can be directly obtained. After adding the port excitation, the mode excitation coefficient (MEC) can be obtained. , mode weighting factor (MWC), different mode excitation power, different mode reflection coefficient and antenna efficiency. In this section, several commonly used line antennas and MIMO antenna PCB boards are listed. The FEKO v14 version software is used to analyze the characteristic modes of the antenna. For wide-band eigenmode analysis, Mode Tracking [8][9] is challenging because the resonant mode changes as the frequency changes. The initial mode number is based on the starting frequency mode. According to the high to low energy, some modes will gradually disappear with the change of frequency (the energy occupancy ratio is getting smaller and smaller), and some new modes will gradually appear. The following examples apply to pattern tracking techniques. Another mode tracking technique is to determine several modes of the starting frequency. Only a few of the determined modes are tracked throughout the wide frequency range, which may lose some new modes. The typical eigenmode analysis process [10] mainly includes three steps: selecting the desired working mode based on the geometric shape mode analysis, selecting the feeding position to add the excitation verification to obtain the desired mode, and verifying whether the parameters of the antenna meet the design requirements. We make OBD connector with terminal by ourselves,
soldering type and crimping type are both available. Also 12V and 24V
type. OBD1, OB2, J1939, J1708, J1962, etc. Also molded by different
type, straight type or right-angle type. The OBD connector cables used
for Audi, Honda, Toyota, BWM, etc. We have wide range of materials
source , also we can support customers to make a customized one to
replace the original ones. Sae J1708 Connector,Sae J1939 Connector,OBD2 Diagnostic Connectors,Diagnostic Connector,Deutsch Diagnostic Connector ETOP WIREHARNESS LIMITED , https://www.wireharness-assembling.com![]() (2.1)
(2.1) ![]() (2.2)
(2.2) 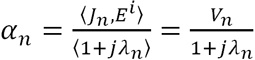 (2.3)
(2.3) ![]() (2.4)
(2.4) ![]() At the total current
At the total current ![]() The importance of this is called the Modal WeighTIng Coefficient (MWC).
The importance of this is called the Modal WeighTIng Coefficient (MWC). ![]() For the characteristic current, λn is the eigenvalue and Ei is the incident field. In Equation 2.4, Vn is the mode excitation coefficient Modal ExcitaTIon coefficient (MEC), and when the excitation signal is added, it is determined which mode is easily excited.
For the characteristic current, λn is the eigenvalue and Ei is the incident field. In Equation 2.4, Vn is the mode excitation coefficient Modal ExcitaTIon coefficient (MEC), and when the excitation signal is added, it is determined which mode is easily excited. 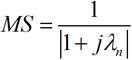 (2.6-1)
(2.6-1) 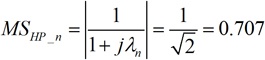 (2.7-1)
(2.7-1) 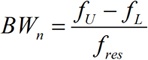 (2.7-2)
(2.7-2)
Antenna design based on eigenmode theory and CMA technology
I. Overview