Abstract: A method for extracting image character features based on wavelet and entropy is proposed. This method uses wavelet transform to decompose the image characters at multi-scale, and uses the marr zero-crossing edge detection operator to extract the edge; extracts the boundary features of each scale image based on the minimization of discriminant entropy. The combination of features that accurately express various types of overlapping conditions and can directly express the error rate. Compared with other methods, the feature vector extracted by this method is stable, the recognition rate is high, and the algorithm is fast, which is very conducive to classification, and the feature extraction method has the characteristics of human vision. Online signature verification is a technology that collects and verifies personal signatures through a computer to achieve a paperless office [1]. Among them, extracting effective special characters from the collected video images is the core step of the online signature verification system. With the rapid development of computer and pattern recognition technology, there have been many schemes for extracting character features, the most representative ones are edge description method and moment description method [2]. The method of describing the shape of the edge can be used curve fitting and Fourier descriptor method. Although the Fourier descriptor better describes a closed image outline, it has many features, and noise and quantization errors have a greater impact on coefficients with lower amplitudes. When FFT is used to calculate the Fourier coefficients, the length of its boundary points must be rounded to an integer power of 2, and its description does not have three (direction, position, size) invariance. It cannot be directly used for target recognition and must be complicatedly transformed . These have affected its use. The moment description method is to use the moments of the gray distribution of the image to describe the characteristics of the gray distribution of the image. The moment feature is a double integral defined in the entire image space. It also does not have three invariants and must be normalized when used. The invariant moment is just a rotation normalization method, which must be combined with the size and the position normalization process to have three invariances. 1 Wavelet multi-scale decomposition In order to find the basis of L2 of the space, we first start from a certain subspace of L2, establish the basis in this subspace, and then use simple transformation to extend this basis to the space L2 to form a set of basis. This is the multi-scale analysis method [3] [4]. For the two-dimensional case, let {V2J} jez be a separable MRA: V2J = VjVj, where {V2j} jez is an MRA of L2 (R2), and its scale function is ï¿ is one-dimensional MRA {V2j} jez Real-valued scaling function, the wavelet generating function uses Dabuechies [6] wavelet; corresponding to the two-dimensional scaling function V2j = VjVj, three functions are defined: The orthogonal standard basis of the subspace W2j, and their telescopic translation system (abbreviation) is: It is a standard orthogonal basis for L2 (R2). In this system, the signature is collected to the computer and displayed on the screen through the tablet and electronic pen connected to the computer. The image collected and input into the computer is two-dimensional. In this paper, the image to be decomposed is f (x, y) ΕL2 (R2). For convenience, let L2 (R2) -V2N, let fN be the orthogonal projection of f on V2N. In this way, the finite wavelet decomposition of f is the decomposition of fN. due to: Suppose the scaling function Φj, Φj (x, y) = 2jΦ (2jx, 2jy) on {V2j} jez is the scaling function of the two-dimensional MAR {V2j} jez, the wavelet function ψ (α) j, α = 1,2, 3 has been given by equation (1) and equation (2) respectively, and by the array {CNk1, k2}, (k1, k1ΕZ2), such that: Among them, Cn, k1, k2 = Similarly, there are: In the formula (6), j = N-1, Λ, NM. fj is the low-pass filtered signal of fN on f2j, and gαj, α = 1,2,3 are the three high-pass filtered details of fN on W2j. Then, the length-limiting sequences {Pk1} and {Pk2} are high-pass filter coefficients in the x and y directions on the plane (x, y), and {gk1} and {gk2} are low-pass filter coefficients in the x and y directions , Then from equation (6): The right part of the arrow in the above formula is the matrix representation of the left part, where CN is the distribution array of the original signal f (x, y), Pr and Pc are operators that perform low-pass filtering on the rows and columns of CN, and Qr, Qc is an operator that performs high-pass filtering on the rows and columns of CN, respectively. And the j-th decomposition should be: In equation (7), j = N-2, Λ, NM. Equation (7) is the Mallat tower algorithm for finite orthogonal wavelet decomposition of two-dimensional signals fN or CN [5]. Through experiments, the use of Daubechies 8 wavelet can achieve a better decomposition effect. The wavelet decomposition of the real signatures and forged signatures collected into the computer is limited to the breadth. This article only gives a decomposition diagram of the real signatures, as shown in Figure 1. Usually in experiments, with the help of Matlab 6.5, the character images of true and false signatures are passed through two complementary filters, namely a low-pass filter and a high-pass filter, to obtain the similar and detailed parts of the image, respectively. Similar sub-pictures are mainly the global and low-frequency components of the original image, while detailed sub-pictures are usually the local and high-frequency components of the original image. The detail sub-picture includes three parts: horizontal sub-picture, diagonal sub-picture and vertical sub-picture. The detail sub-picture is filtered twice: the low frequency component is allowed to pass in the horizontal direction, and the high frequency component is allowed to pass in the vertical direction. This is enhanced for horizontal strokes (gradation changes are low frequency in the horizontal direction and high frequency in the vertical direction), while vertical strokes (gradation changes are high frequency in the horizontal direction and low frequency in the vertical direction) are smooth. The pixels in the vertical and oblique directions are highlighted in the vertical sub-picture and the oblique sub-picture, respectively, for the same reason. This direction selectivity is consistent with the visual characteristics of the human eye, so that the characteristics based on this algorithm are similar to the visual characteristics of the algorithm. Classic edge detection operators include Sobel operator, Laplace operator, Marr operator, etc. In recent years, some scholars have proposed generalized fuzzy operators [7], morphological edge operators [8], etc. The Marr edge detection operator 2G is known as one of the best edge monitors, so this article uses the Marr operator. The characteristic of this operator is to use Gaussian filter to smooth the image. Response function of two-dimensional Gaussian filter The above operator is used to convolve the image, and the position of the zero crossing point is determined by judging the change of the sign, which is the edge point. The processing result of the real signature after wavelet decomposition is shown in Figure 2. It can be seen from Figure 2 that the Marr zero-crossing edge operator extracts strong and weak edges at the same time, and the edges are relatively clean, with less noise interference and good continuity. 3 Feature extraction based on discriminant entropy minimization Different samples occupy different regions of the feature space, as long as these regions do not overlap, they can be separated. The average distance between samples is often used as the criterion function for feature extraction. Important distances include Minkowski metric ΔM, Euclidean distance δE, Chebychev distance δr, squared distance δQ, and nonlinear metric δN. Without considering various types of probability distributions, it is not possible to accurately express various types of overlapping conditions, and the error rate cannot be directly expressed. For this reason, the probability distance should be considered, and the classification with the least uncertainty is the most advantageous. Therefore, the entropy can be used to measure and verify the centralized procedure of the probability distribution. Some measure of the degree to which the probability distribution density deviates from a given standard distribution is called relative entropy. This paper assumes that the probability distribution of the image function processed by wavelet and Marr operator (xi, yj) is P (xi, yj). Given the standard distribution ω (xi, yj), the relative entropy between the two is : The summation should be performed on all possible values ​​of this feature. The smaller the relative entropy, the greater the difference between the two types of probability distribution. When the two types of probabilities are exactly the same, the relative entropy reaches the maximum value (equal to zero). Therefore, the discriminant entropy W (p, q) can be defined to characterize the difference between the two types of distributions p (xi, yj) and q (xi, yi). In the case of multiple categories, ΣnΣmW (p (n), q (m)) can be used to denote the degree of separation between various types of distribution. Here n, m represent the category number. For feature extraction, given the dimension d, such d features are obtained, which minimizes the above-mentioned discriminant entropy. For the convenience of calculation, this paper uses the following function -U (p, q) = ΣiΣj (pi, j-qij) 2≤0 instead of W (p, q) without affecting the result of selecting d optimal features. When the probability distribution is not estimated, the normalized sample feature value can be used to replace the probability distribution in the above formula. K is the sample number in the first type of sample set, N1 is the total number of samples in the first type, and i is the feature number. due to It can be seen from the calculation data in Tables 1 and 2, that the minimum discriminant entropy data after one-time decomposition of wavelet can clearly identify the true and false signatures. Moreover, the minimum discriminant entropy of similar graphs and detail graphs is very different, and the difference is large; while the minimum discriminant entropy of the three parts of horizontal sub-picture, oblique sub-graph, and vertical sub-graph in the detail graph is small. Therefore, the feature vectors extracted in this way have good stability, great distinction and high accuracy. Table 2 Minimum Discriminant Entropy of Forged Signature 4 Experimental conclusion Experiments were conducted on 120 different real signatures, and each real signature corresponds to 20 different forged signatures. These signature images were decomposed 6 times with wavelet, and 256 images were selected for edge connection and minimum respectively. With the feature extraction of discriminant entropy, the discrimination rate reached 98.7%, and satisfactory results were obtained. The above theoretical analysis and experimental verification show that using wavelet decomposition to decompose the original single time-domain signal into signals at different frequency scales can not only obtain detailed information of the image at various scales, but also have less noise interference and clear edges; When extracting, the expected value of the entropy function is used to characterize the degree of separation of the categories, which can be used as an evaluation of classification effectiveness. The superiority of this method is of great significance for improving the accuracy of online signature verification. Follow WeChat Download Audiophile APP Follow the audiophile class related suggestion
figure 1
Although the use of these features for image recognition has achieved satisfactory results, the definition of these features is quite complicated, requires a lot of calculations, and is completely different from the human cognition mechanism, which cannot be intuitively understood. This paper proposes a new idea of ​​combining statistical features and structural features, and performs wavelet multi-scale decomposition on character images, which effectively suppresses the noise in the image and fully reflects the fine features of the image structure; Feature extraction can accurately express all kinds of overlapping conditions, and can directly express the error rate, thereby effectively improving the recognition rate. 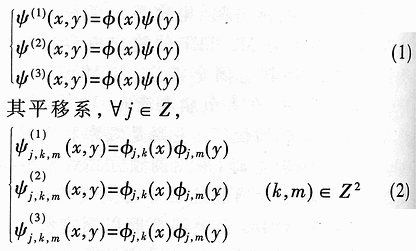
![]()
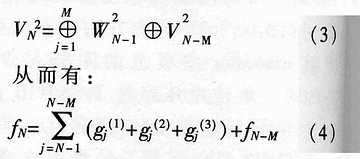
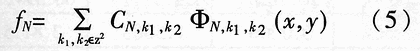
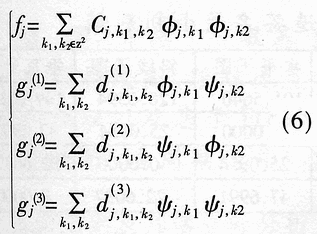
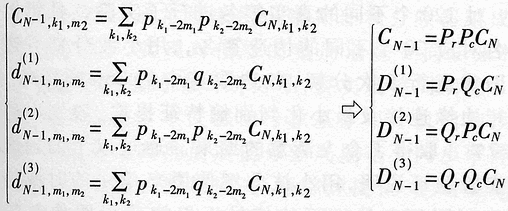
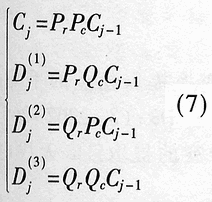
figure 2
2 Zero crossing edge operator 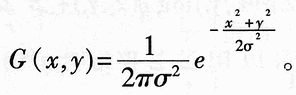 . Let f (x, y) be a binary image function. From the interchangeability of convolution and differentiation in a linear system, we get â–½ 2 {G (x, y) Ñ…I (x, y)} = {â–½ 2G (x, y)} Ñ…I (x, y), that is, the Gaussian smoothing filter and Laplacian differential operation of the image can be combined into a convolution as follows:
. Let f (x, y) be a binary image function. From the interchangeability of convolution and differentiation in a linear system, we get â–½ 2 {G (x, y) Ñ…I (x, y)} = {â–½ 2G (x, y)} Ñ…I (x, y), that is, the Gaussian smoothing filter and Laplacian differential operation of the image can be combined into a convolution as follows: 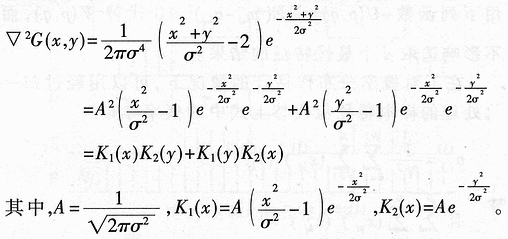
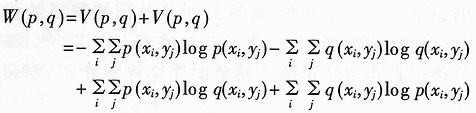
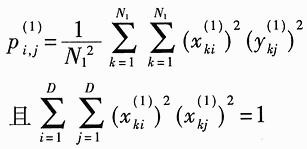
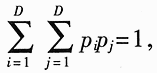 , This is reasonable. The coordinate system engineering where U takes the minimum value is made up of d eigenvectors corresponding to d eigenvalues ​​that satisfy certain conditions in the matrix A = G (1) -G (2). Here G (1) and G (2) are the covariance matrix of the first type sample set and the second type sample set respectively. That is, the eigenvalues ​​λk, k = 1,2, ΛD corresponding to the eigenvector uk of the matrix A are queued:
, This is reasonable. The coordinate system engineering where U takes the minimum value is made up of d eigenvectors corresponding to d eigenvalues ​​that satisfy certain conditions in the matrix A = G (1) -G (2). Here G (1) and G (2) are the covariance matrix of the first type sample set and the second type sample set respectively. That is, the eigenvalues ​​λk, k = 1,2, ΛD corresponding to the eigenvector uk of the matrix A are queued: ![]() The eigenvector corresponding to the eigenvalue is selected as the required coordinate axis system, and the discriminant entropy is the smallest in this coordinate system. Select Shannon entropy in the experiment. Table 1 and Table 2 list the minimum discriminant entropy of each scale image after decomposition of real signature and forged signature, respectively.
The eigenvector corresponding to the eigenvalue is selected as the required coordinate axis system, and the discriminant entropy is the smallest in this coordinate system. Select Shannon entropy in the experiment. Table 1 and Table 2 list the minimum discriminant entropy of each scale image after decomposition of real signature and forged signature, respectively.
Table 1 Minimum Discriminant Entropy of Real Signature Similar graphics Horizontal subgraph Diagonal subgraph Vertical subgraph Similar graphics 0.0000 56.7827 58.371 60.5942 Horizontal subgraph 58.371 0.0000 1.5883 3.8115 Diagonal subgraph 56.7827 1.5883 0.0000 2.2232 Vertical subgraph 60.5942 3.8115 2.2232 0.0000 Similar graphics Horizontal subgraph Diagonal subgraph Vertical subgraph Similar graphics 0.0000 101.5640 126.6594 149.2631 Horizontal subgraph 101.5640 0.0000 25.0954 47.6991 Diagonal subgraph 126.6594 25.0954 0.0000 22.6037 Vertical subgraph 149.25631 47.6991 22.6037 0.0000 


'+ data.username +'
Improvement of image character feature extraction method based on wavelet multi-scale and entropy
Interesting and informative information and technical dry goods
Create your own personal electronic circle
Lock the latest course activities and technical live broadcast
comment
Publish