In 1996, Lowe first used the communication sequence process CSP and model detection technology to analyze the NSPK (Needham-Schroeder Public Key) protocol, and successfully discovered a man-in-the-middle attack in the protocol. Subsequently, Roscoe conducted a further study on the combination of CSP and FDR (Fallures-Divergence Refinenent), and believed that the CSP method is a new way to formally analyze security protocols. Facts have proved that the CSP method is very effective for security protocol analysis and discovery of security protocol attacks. However, FDR-like model detection is usually limited by the size of fresh values ​​such as NONce and Key, and the data value required in actual execution is much larger than this. The use of data-independent technology enables nodes to call unlimited fresh values ​​to ensure an unlimited sequence of instances. This article will study these theories of Roscoe and design and implement the CSP protocol model to solve the problem of limited detection. 1 CSP protocol model The CSP protocol model consists of some trusted participant processes and intruder processes. The processes run in parallel and interact through channels. Take the NSPK protocol as an example. The CSP model of the protocol includes two agents (initiator a, responder b) and a server s that can perform key generation, transmission or authentication services, and they communicate through untrusted media (intruders) Four CSP processes. The CSP process of IniTIator a is described as follows: Responder b and server s have similar descriptions. 2.1 Independent analysis of general data In general, independent data analysis finds a finite threshold for verification problems with type T as a parameter. If the system can be verified for the threshold of T, then the system can also be verified for all larger T values. This is true for many problems. Many features in the security protocol model can be regarded as data independent entities. Common keys and nonces can be used as parameters of the process in the model. Threshold calculations for security protocols that rely on the uniqueness of nonce and keys (and other simple data objects that rely on the protocol) are mainly to discover the threshold of process storage, which cannot directly solve the limitations of verification and cannot be directly applied The security protocol model. 2.2 Roscoe's data independent technology (1) Basic principles This inequality only applies to variables, and the situation is different for constants in the program. Therefore, the following two conditions are proposed: The process of the non-single mapping function again satisfies equation (1). Some aspects of the protocol may not satisfy the PosConjEqT condition. For example, the agent process may need to perform inequality tests with constants (such as names). Therefore, the PosConjEqT′c condition is defined for the constant set C as follows: 10.1 Inch Laptop,win10 Laptops,win11 Laptops Jingjiang Gisen Technology Co.,Ltd , https://www.jsgisengroup.com
In the CSP model, protocol participants are represented as CSP processes, messages are represented as events, and protocols are represented as a set of communication sequence processes. 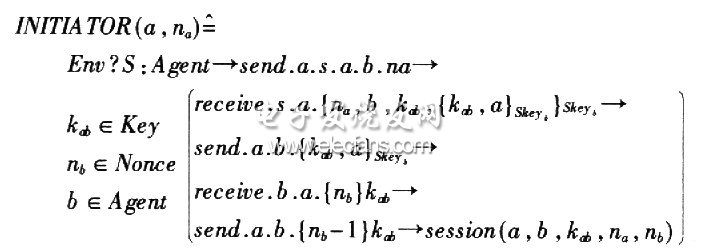
The attacker process is described as: 
2 Data independent technology
Data independent technology is the key technology of this paper. It originated from independent research of Lazic data.
If a process P has no restrictions on type T, then P is data independent on type T. At this time, T can be regarded as a parameter of P.
The previous section proved that the data-independent results of the general goal are not suitable for the analysis of security protocols. So Roscoe makes inferences about these results. Developed data independent technology. This section will introduce several inferences that have important theoretical significance for the research of the subject.
The basic principle on which the inference of general data independent analysis results is based is also the most important method to prove the data independent theory. That is, to establish a mapping relationship by applying the Conapsint function φ to the parameter type T of the process P, it is proved that the behavior of P (T) before mapping is a subset of the behavior of P (φ (T)) after function conversion.
The trace of the main research process for the security protocol. It can be intuitively found that if the Collapsing function φ is single-mapped (all members of T are mapped to different values) and applied to the parameter type T of the process P (P is independent of T data), because all members of T are The mapping is different values, so the behavior before mapping is equivalent to the behavior after mapping, as shown in equation (1): 
If the Collapsing function φ used is a non-single mapping function, it is possible to change the equivalent test result and produce an inequality (2): 
The PosConjEqT (PosiTIve ConjuneTIons of Equality teSTs) condition is proposed by Lazic, which can make the variable use
Although constants cannot satisfy equation (1) again, they can satisfy inequality (3): 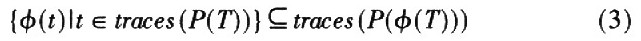
If the process P satisfies the following conditions for the constant set C, it is said that the process P satisfies the PosConjEqT′c condition. This condition satisfies the PosConjEqT condition, but the difference from the PosConjEqT condition is that for an equivalent test that contains at least one member of the constant set C, P may have a non-STOP result.